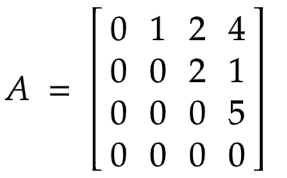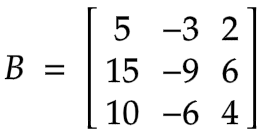What is Nilpotent Matrix?
Nilpotent matrix: Any square matrix [A] is said to be a Nilpotent matrix if it satisfies the condition [Ak] = 0 and [Ak-1] ≠ 0 for some positive integer value of k. Then the least value of such positive integer k is called the index (or degree) of nilpotency. If the square matrix [A] is a Nilpotent matrix of order n x n, then there must be Ak = 0 for all k ≥ n. For example, a 2 x 2 square matrix [A] will be Nilpotent of degree 2 if A2 = 2. In general, any triangular matrix with zeros along with its main diagonal is a Nilpotent matrix. A nilpotent matrix is also a special case of the convergent matrix.
Example of Nilpotent Matrix
Here in this triangular matrix, all its diagonal elements are zero. Also here A4 = 0 but A3 ≠ 0. So [A] will be a nilpotent matrix of order or degree 4.
Here in this 3 x 3 matrix B2 = 0 but B1 ≠ 0, although it has no zero diagonal elements. Hence [B] will be a nilpotent matrix of order 2.
Properties of Nilpotent Matrix
The following are the important properties of a nilpotent matrix.
- A nilpotent matrix is a square matrix and also a singular matrix.
- The determinant and trace of Nilpotent matrix will be zero (0).
- If [A] is a Nilpotent matrix then [I+A] and [I-A] will be invertible.
- All eigenvalues of Nilpotent matrix will be zero (0).
- If [A] is a Nilpotent matrix then the determinant of [I+A] = 1, where I is n x n identity matrix.
- The degree or index of any n x n Nilpotent matrix will always be less than or equal to ‘n’.
- For Nilpotent matrices [A] and [B] of order n x n, if AB = BA then [AB] and [A+B] will also be Nilpotent matrices.
- Every singular matrix can be expressed as the product of Nilpotent matrices.
Characterization of Nilpotent Matrix
For any n x n square matrix [A], the following are some important characteristics observed.
- Square matrix [A] is a Nilpotent matrix of degree k ≤ n (i.e., Ak = 0 ).
- The characteristics polynomial of [A] will be det(xI – A) = xn
- The minimal polynomial of [A] will be xk provided k ≤ n.
- The only (complex) Eigenvalue of [A] is zero (0).
- Trace (Ak) = 0 for all k > 0 i.e., the sum of all diagonal entries of [Ak] will be zero.
- The only Nilpotent diagonalizable matrix is the zero matrix.
How to find the index of the Nilpotent Matrix
According to the definition, if a square matrix [A] is a Nilpotent matrix then it will satisfy the equation Ak = 0 for some positive values of ‘k’, and such smallest value of ‘k’ is known as the index of the Nilpotent matrix. So to find the index of the Nilpotent matrix, simply keep multiplying matrix [A] with the same matrix until you get a zero matrix or null matrix (0). For example suppose you multiplied matrix [A], k times and then you got Ak = 0. Hence the index of that Nilpotent matrix [A] will be that integer value k.
There is a guarantee that the index of n x n Nilpotent matrix will be at most the value of n. So you will have to multiply the matrix maximum n (order of matrix) times.
Read More:
- Involutory matrix and its properties
- Idempotent matrix and its properties
- Core balance CT (CBCT) or zero sequence CT (ZCT)
- Power Factor Correction techniques
- Surge impedance loading (SIL) of Transmission line
- What is power factor and why it is important
- Different Parts of transformer and their functions
- Theory and working of Star-Delta Starter